树的直径

求一个自由树的直径。对于直径，《算法导论》第三版 349 页练习 22.2-8 上面这么定义道：

树中所有最短路径的最大值即为树的直径。

这个树由于没有根结点，其实直径这个概念，还是理解为一个连通无向无环图的直径为好。

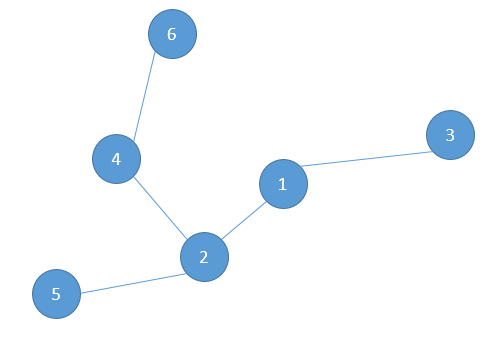
现在给定如下格式的输入：

8
1 2
1 3
1 4
4 5
3 6
6 7
7 8

第一行是这个图的结点个数，不妨记为 N，以下 N-1 行是 N-1 条边，结点序号按照 1-N 顺序编号。求这个图的直径。

这个输入的输出结果是 6，给出这个示意图就可以看得很清楚：

对于这个问题，最笨的方法就是对每一个结点进行 BFS，因为 BFS 有这个性质：BFS 生成的 广度优先树的每一个结点到达根结点的路径总是最短路。这样，把每一个结点 BFS 一遍就会生成一个该结点到达的最远结点。按照定义取出最长的路径即可。由于 BFS 时间复杂度是 O(N)，这个方法的时间复杂度是$O(N^2)$。

其实还有一个更为简便的方法：首先对任意一个结点做 BFS 求出最远的结点，然后以这个结点为根结点再做 BFS 到达另一个最远结点。第一次 BFS 到达的结点可以证明一定是这个图的直径的一端，第二次 BFS 就会达到另一端。下面来证明这个定理。

但是在证明定义之前，先证明一个引理：

引理：在一个连通无向无环图中，x、y 和 z 是三个不同的结点。当 x 到 y 的最短路与 y 到 z 的最短路不重合时，x 到 z 的最短路就是这两条最短路的拼接。

证明：假设 x 到 z 有一条不经过 y 的更短路$\delta (x,z)$，则该路与$\delta (x,y)$、$\delta (y,z)$形成一个环，与前提矛盾。

定理：在一个连通无向无环图中，以任意结点出发所能到达的最远结点，一定是该图直径的端点之一。

证明：假设这条直径是$\delta (s,t)$。分两种情况：

1. 当出发结点 y 在$\delta (s,t)$时，假设到达的最远结点 z 不是 s,t 中的任一个。这时将$\delta (y,z)$与不与之重合的$\delta (y,s)$拼接（也可以假设不与之重合的是直径的另一个方向），可以得到一条更长的直径，与前提矛盾。
2. 当出发结点 y 不在$\delta (s,t)$上时，分两种情况：

1). 当 y 到达的最远结点 z 横穿$\delta (s,t)$时，记与之相交的结点为 x。此时有$\delta (y,z)=\delta (y,x)+\delta (x,z)$。而此时$\delta (y,z)>\delta (y,t)$，故可得$\delta (x,z)>\delta (x,t)$。由1的结论可知该假设不成立。

 2). 当 y 到达的最远结点 z 与$\delta (s,t)$不相交时，记 y 到 t 的最短路首先与$\delta (s,t)$相交的结点是 x。由假设$\delta (y,z)>\delta (y,x)+\delta (x,t)$。而$\delta (y,z)+\delta (y,x)+\delta (x,s)$又可以形成$\delta (z,s)$，而$\delta (z,s)>\delta (x,s)+\delta (x,t)+2\delta (y,x)=\delta (s,t)+2\delta(y,x)$，显然与题意矛盾。

因此定理成立。

9月21日补充：这道题是上一周 hihocoder 上面的一道题。出题者的原意并不是要我们这么做。出题者写了很长的一段提示，但是这段提示的语文表述很差，完全没有抓住重点，导致我花了一个星期的时间也没弄明白他在讲什么。现在所有人的源代码均已公开，可以继续下去了。

出题者的原意是要我们使用这么一个定理：

定理2：树的直径，等于以树直径上任意一点为根的有根树，其左子树的高度+1，再加上其右子树高度+1。

按照这种定理的定义，我们可以设计这样一个程序，对每个结点计算左子树高度+右子树高度+2.这样的时间复杂度是$O(n^2)$。由于我们不知道所选取的结点是否是在直径上，所以要进行这样的枚举。显然这会超时。但是根据本文的提示，寻找这种直径的过程其实可以递归化：

1. 在根结点的左子树上；
2. 在根结点的右子树上；
3. 直径经过根结点。

于是我们可以设计这样的程序：选取任意结点为根结点，递归地计算每个结点的高度。在结点内部计算高度的同时，计算以当前结点为根的子树的左子树高度+右子树高度+2，用于更新全局树直径。